在高中时，我无数次计算过e这个数。它常常伴随着各种奇奇怪怪的函数，方程出现。但老师只教过我怎样去算它，e约等于2.718…e的导数还是e……

我也一直难以理解这个数，直到一次偶然机会，我才发现，e真是太神奇了！

e的历史

我们在百度百科上搜一下”e”，解释是：

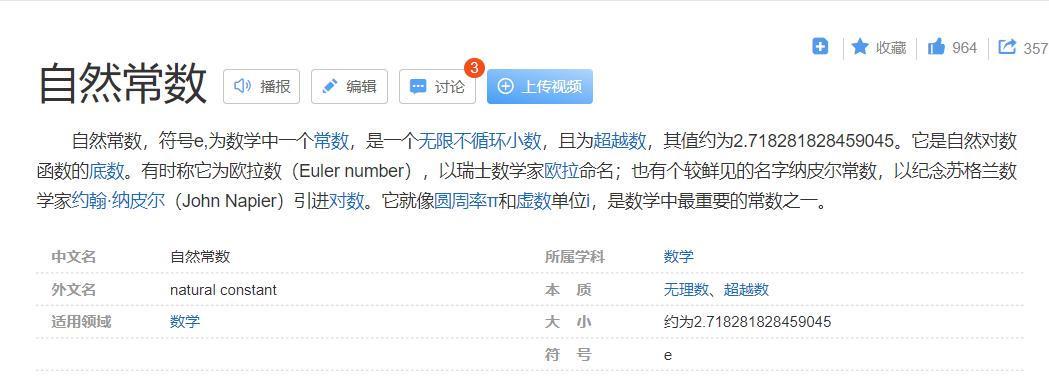
数学对它的定义是“自然常数”。我对于常数的理解一直是，不会随着时间变换而变换的数。它就像明天一定会到来一样固定。

但它为什么自然呢？

简单比喻

我们以银行存钱来比喻。银行存钱一般以年利率来计算，存一块钱，年利率3%。一年后就可以得到1.03块钱。

我们假如有一个银行的利率是100%，那么，存1块钱，在一年后就应该得到2块钱。

而利率是可以拆分的，年利率可以拆分为月利率，月利率下面还有七日利率。

我们一块钱存半年，可以得到1.5元。我们再投资，1.5再存半年，应该得到1.5*(1+50%)=2.25。

没错，我们的钱钱变多了😛

如果银行允许我们无限操作，那么，我想我有了一个大胆的想法😎。

但把时间拆成无数份，我们存了再取，取了再存。我们的钱钱是否真的会无限变大呢？

我们存一年，利率公式为1(1+100%)=2
一年分为两个时间段，利率公式为1(1+50%)²=2.25
一年分为三个时间段，利率公式为1(1+33%)³=2.352
一年分为四个时间段，利率公式为1(1+25%)⁴=2.441
……

时间是无限份的，我们就可以得到$\displaystyle\lim_{x\to+\infty}\left(1+\frac{1}{x}\right)^x$极限公式(第二重要极限😛)

我们对它求一下极限，它其实就是e。

我们将x带入值计算y=$\displaystyle\lim_{x\to+\infty}\left(1+\frac{1}{x}\right)^x$。也会发现，在y短暂的快速变化后，y值变化的速度越来越小，开始无限趋近于2.718…..

它就是e

很久之前，我的小外甥女问我树是什么时候长高的。我说在晚上你睡着了它就开始悄悄长高了。

那它是突然一下就长高了呢还是一直在长呢？

一直在长高呢，就像你长个子一样，每时每刻都在长。

那现在它又长高了多少呢？

….

是阿，时间是无限的，是不可分割的。相比起上一刻，我们又变化了多少呢？

我想，现在有了答案。我们变化了e